Try to understand Monad, again.
By Yichao Ma at
Disclaimer: Contents below are my own understanding on the topic discussed. They might be correct or wrong. Take my words with a grain of salt and feel free to point out the mistakes.
Coming from an Object-Oriented Programming (OOP) background. I still remember the very first time I was exposed to Functional Programming (FP). My mind was blown after seeing people define small functions and compose them in different ways to get different results while keeping the code elegant and easy to read. I had absolutely no idea why things worked together magically. But I felt like it opened a door to a whole new world in which people reason about programs with a totally different mental model. After reading the book Professor Frisby's Mostly Adequate Guide to Functional Programming by Brian Lonsdorf (a.k.a. Dr Boolean). I got a basic understanding of how things work under the hood and I started experimenting some of those techniques in the codebase I worked with back then. It made things deterministic and easy to test when you know all these functions that are used to compose a new function are pure functions. And I was really happy with the result I achieved using the knowledge I acquired from another programming paradigm. But still there's one thing that I hear FP people talk about a lot and I don't quite understand what it is: Monad.
In order to understand Monad, I even took a functional programming course which was taught using Haskell during my Master's program. Although I was able to complete the assignments when we focused on the topic of Monad for those ~2 weeks during the semester. But the explanation given by the instructor still didn't make a light bulb go off in my head. After taking the course, all I know about Monad is merely that we need to implement the Functor, Applicaive, and Monad interfaces (or typeclasses shown below) and we can write code using the do-notation. But I still don't know why and when we should make things monadic.
class Functor f where
fmap :: (a -> b) -> f a -> f b
class Functor f => Applicative f where
pure :: a -> f a
(<*>) :: f (a -> b) -> f a -> f b
class Applicative m => Monad m where
return :: a -> m a
(>>=) :: m a -> (a -> m b) -> m bWhy is Monad useful?
Recently, I've been trying to refresh my memory on parsing algorithms and techniques. Then I remember that we were implementing a monadic parser for one of the assignments in that Haskell course back in school. So I decided to give another try to understand Monad. Luckily, this time I found lectures from professor Graham Hutton on Youtube about advanced FP topics in Haskell. The videos focusing on Monad give some good examples of why and when Monad is needed, and I would say they are the best videos I've seen explaining Monad. Let's start with why Monad is useful using the example from the lecture.
Consider that we will be evaluating expressions of divisions between integers. An expression can be represented by the following recursive data type.
data Expr = Val Int
| Div Expr ExprThen a function to evaluate an expression can be defined like this:
eval :: Expr -> Int
eval (Val n) = n
eval (Div e1 e2) = eval e1 `div` eval e2As you can see this function will throw divide-by-zero exception when eval e2 returns zero.
To represent failure in a pure functional language like Haskell. We need a special type to indicate
something could fail. Haskell has a built-in Maybe type (shown below) that can be used in this situation.
data Maybe a = Nothing -- failure with no result
| Just a -- success with result `a`Then we can create a safe version of div and rewrite our eval function like this:
safediv :: Int -> Int -> Maybe Int
safediv _ 0 = Nothing
safediv x y = Just (x `div` y)
eval :: Expr -> Maybe Int
eval (Val n) = Just n
eval (Div e1 e2) =
case eval e1 of
Nothing -> Nothing
Just x ->
case eval e2 of
Nothing -> Nothing
Just y -> safediv x yA key notion mentioned in the lecture is that Monad is about observing common pattern.
And here the pattern in eval is that we have to check the result of eval using case-of branches
for both sub-expressions of Div Expr Expr. Let's extract this common pattern to an infix function
named >>=.
mx >>= f =
case mx of
Nothing -> Nothing
Just x -> f xSo what is the type of >>=? We can infer the type based on the implementation.
Because we are matching mx against Nothing and Just, we know mx must be a Maybe type of
something (i.e. Maybe a). Since we are passing the inner value x of Just x to f.
Then we know f takes a parameter of the same type as x. What should be the result type of f x?
Because both case branches must return the same type. Therefore, f x is also a Maybe type of
something (i.e. Maybe b which means it might not contain a inner value of the same type as x).
With our analysis, we can finally tell that this function has type (>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b.
Let's rewrite our eval again using this helper function >>=.
eval :: Expr -> Maybe Int
eval (Val n) = Just n
eval (Div e1 e2) = eval e1 >>= \x ->
eval e2 >>= \y ->
safediv x yThis can be generalized to any number of parameters as follows:
m1 >>= \arg1 ->
m2 >>= \arg2 ->
.
.
.
mn >>= \argn ->
f arg1 arg2 ... argnWe will only get our final result if every argument to f is obtained successfully. A failure during
the process will terminate the computation early and the whole thing will just evaluate to Nothing.
This is similar to propagating an exception in OOP languages like Java using throw statement.
In fact, this pattern is common enough so Haskell even has a syntactic sugar for it known as the do-notation.
do arg1 <- m1
arg2 <- m2
.
.
.
argn <- mn
f arg1 arg2 ... argnLet's rewrite our implementation using the do-notation.
eval :: Expr -> Maybe Int
eval (Val n) = Just n
eval (Div e1 e2) = do x <- eval e1
y <- eval e2
safediv x yYou probably have already noticed that the function >>= defined above has a very similar type as
the >>= method defined on typeclass Monad. Actually, Maybe type does implement the Monad typeclass
and we can use >>= (known as the bind operator) directly without having to define our own implementation.
Try the following in GHCi from command line and see if you get same output.
$ ghci
λ> Just 10 >>= \n -> Just (n*2)
Just 20
λ> Just 10 >>= \_ -> Nothing >>= \n -> Just (n*2)
NothingNow we see that Monad can help us "bind" operations together and deal with effects in a pure language.
And we are able to leverage the do-notation to improve code readability. The lectures also give
more examples of making other types monadic. Among those examples, I find the state Monad to be a
really good case when Monad should be used.
Tree labeling
Assume we have the following tree structure. Our task is to assign a unique label to each leaf.
data Tree a = Leaf a
| Node (Tree a) (Tree a)Taking the approach from the lecture, we will use integers as labels. To make sure all labels assigned are unique, we just need to start from a particular value (e.g. zero), and keep incrementing it every time we assign the current value to a tree leaf. This can be done easily in an imperative programming language by mutating a variable while traversing the tree. But values in Haskell are immutable. Then how can we update the label (or state in general) in a pure functional language?
Basically, what we are trying to achieve is to have a value representing the current state, and another thing to transform the current state into a new state. Since we are using integers as labels. Then our state would be an integer representing the next available label. This part is straightforward.
type State = IntTo update our state, we need to find a way to accomplish the same effect given by State = State + 1
as in an imperative language. Since we are in the FP world. Then function would naturally be our resort.
We need a function that takes the current state as input. The output would be a pair in which the
first element is a value produced by current state, and the second element is the next state. This
function transforms the state, therefore it's called a state transformer.
newtype ST a = S (State -> (a, State))
xfm :: ST Int
xfm = S (\n -> (n, n+1))For people who are familiar with state machines,
Elm architecture, or Redux.
You can view this state transformer as transition function, update function, or reducer, respectively.
With this state transformer, we are able to define a monadic function mlabel to label the leaves
in a tree like this:
mlabel :: Tree a -> ST (Tree Int)
mlabel (Leaf _) = do n <- xfm
return (Leaf n)
mlabel (Node l r) = do l' <- mlabel l
r' <- mlabel r
return (Node l' r')Then we can expose a more friendly function label (with a helper function app) so the callers
who want to label a tree don't need to know what this state transformer is all about.
label :: Tree a -> Tree Int
label t = fst $ app (mlabel t) 0
app :: ST a -> State -> (a, State)
app (S f) s = f sIf you call the label function with a tree now, you will get an error because we are using the
do-notation but we still haven't implemented the methods required by those typeclasses to make our
state transformer monadic. Based on the typeclass signatures above.
A type can be a Monad if it's Applicative, and a type can be Applicative if it's a Functor.
So let's make our ST an instance of those one by one starting from Functor.
Functor only requires the fmap method to be implemented. From the signature, we know that it will
take a mapping function (a -> b), and a type constructor f a, then it will return f b. So all
we need to do is extract the a from f a and pass it to the mapping function to get b and put
it back to the same constructor to get f b.
instance Functor ST where
fmap f (S st_a) = S (\s -> let (a, s') = st_a s in (f a, s'))Applicative needs two methods. pure is simple as it takes a value of arbitrary type a and we
just need to put it in a constructor (i.e. ST in our case). I believe this operation is known as lifting.
The other method is sequential application <*>. The function signature looks like fmap but be
careful that the first argument has type f (a -> b) instead of (a -> b). So the logic would be
similar to fmap except we also need to extract (a -> b) from f (a -> b).
instance Applicative ST where
pure a = S (\s -> (a, s))
(ST st_f) <*> (ST st_a) = S (\s -> let (f, s') = st_f s
(a, s'') = st_a s'
in (f a, s''))Finally we can make our state transformer a Monad by implementing the return and bind (i.e. >>=)
methods. return simply injects a value into our monadic type so we can use pure here as well.
The only thing I want to point out is the second argument of >>= has type (a -> m b) which means
that it returns a ST using the a extracted from the first argument m a.
We will use the same helper function
appdefined above again.
instance Monad ST where
return = pure
(S st_a) >>= f = S (\s -> let (a, s') = st_a s in app (f a) s')Now we have everything set up. Try pass a tree to the label function and see if the leaves get
labeled correctly.
$ ghci <your_file_name>.hs
λ> label (Node (Node (Leaf 'a') (Leaf 'b')) (Leaf 'c'))
Node (Node (Leaf 0) (Leaf 1)) (Leaf 2)The benefit of this state transformer is that it handles state changes behind the scene. I really
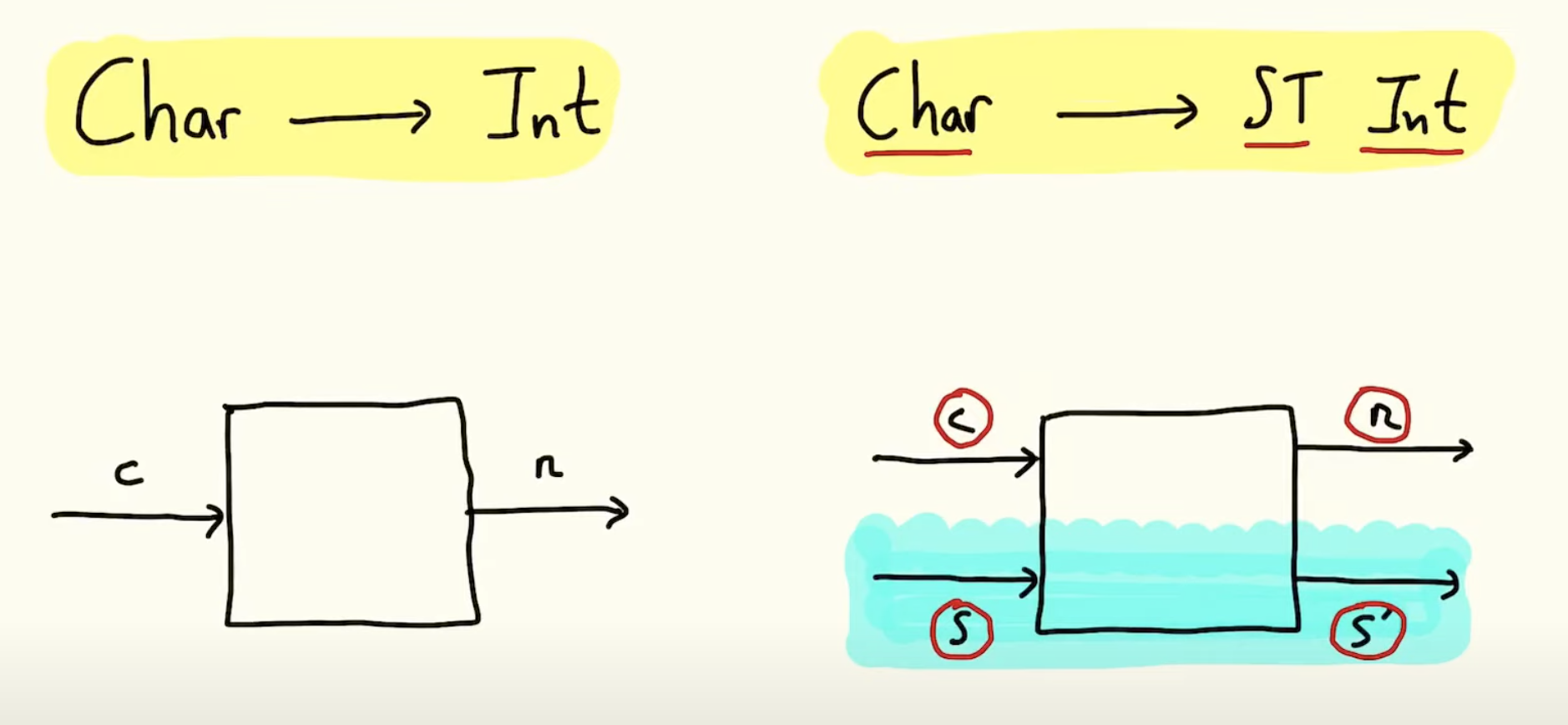
like the way professor Graham Hutton illustrates this mental model in the lecture by drawing pictures
like the one shown below. The types Char and Int in the function definition tell you the input
and output types. The state management done by our state transformer is completely under the water
so the details won't be visible to the user and they can focus on things they care about.
Conclusion
Like being emphasized in the lectures. Monad is about recognizing patterns. A pattern then can be
used to define a generalized idea to solve a class of problems which to me is really powerful.
The state transformer mentioned above takes an initial value, then each new state is merely derived
based on the previous state like a generator. But we can definitely enhance it so it can take other
inputs that can be used while computing the next state. I also noticed that there's a Control.Monad.ST
library that you can import. I assume it provides a more generalized state management approach so
we don't have to repeat ourselves. Please check out the items listed in references to discover more.